728x90
NonSerial Monadic DP : next level의 optimal solution을 계산하기 위해서 바로 이전 level의 optimal subsolution이 아닌 다른 것을 사용 + functional equation에 재귀 식이 한번 사용되는 경우.
예제 문제1) Longest-Common-Subsequence
문제 설명 : 두 문자열의 최장 공통 부분수열을 찾는다.
>> 문자열 같은 부분 건너뛰기 가능

fuctional equation
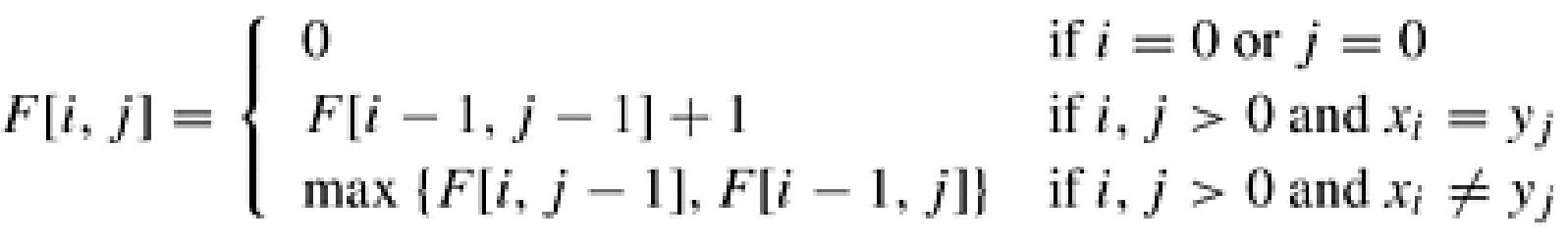
F[i, j] : 한 문자열의 i index 까지, 다른 문자열의 j index 까지의 최장 공통 부분수열의 길이를 저장.


* Table entries are computed in a diagonal sweep from top-left to the bottom-right corner.
- 왼쪽 위 대각선부터 오른쪽 바닥 대각선 까지 차례대로 계산해 나간다.
>> 각 대각선이 각 level을 나타낸다.
F[i, j]를 계산하기 위한 dependancy를 봤을 때 바로 이전 level의 값과 두 단계 이전 level의 값이 사용되기 때문에 nonserial, 3가지 이전 단계 재귀 식중 하나를 사용하기 때문에 monadic이다.
Parallel
n개의 processing elements 들이 table의 각 column을 계산한다.
PRAM의 경우 테이블 F의 원소에 모두 상수시간에 접근가능하고, 단계가 2n - 1개이기 때문에 시간 복잡도는 O(n)이다.
이 병렬이 cost optimal 한가?
O(n) 에 processing elements 개수 n을 곱하면 n^2 인데 이는 serial 하게 처리한 경우의 시간 복잡도와 동일하기 때문에 cost optimal 하다고 보는 것 같다. << (추후 확인 필요)
'병렬처리' 카테고리의 다른 글
| Parallel computing (Dynamic Programming) - 5 / Nonserial Polyadic DP (0) | 2022.12.27 |
|---|---|
| Parallel computing (Dynamic Programming) - 4 / Serial Polyadic DP (0) | 2022.12.26 |
| Parallel computing (Dynamic Programming) - 2 / Serial Monadic DP (0) | 2022.12.26 |
| Parallel computing (Dynamic Programming) - 1 (0) | 2022.12.26 |
| 내가 보기 위한 OpenMP 사용법 (0) | 2022.10.27 |